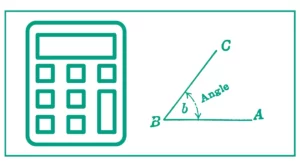
Arccos Calculator

Enter X Value:

The arccos calculator helps you calculate the inverse cosine function arccos in degrees and radians.

Enter the x value between -1 and 1 to calculate the arccos.

Inverse cosine, or arccosine, is the inverse of the cosine function. It measures the unknown angle when the lengths of two sides of a right triangle are known. It is also abbreviated as 'arccos'.

arccos x = cos-1x

You might want to find the foci or calculate the cosecant.

What is Inverse Cosine?

Before diving into the calculator itself, it's crucial to understand what inverse cosine means. The inverse cosine, often written as arccos or cos^(-1), is a mathematical function that returns the angle whose cosine is a given value. It's the reverse operation of the cosine function.

In simpler terms, if you have a cosine value and want to find the corresponding angle, you use the inverse cosine function. This is particularly useful in trigonometry and related fields where determining angles from known ratios is necessary.

How to Use the Inverse Cosine Calculator

Using an inverse cosine calculator is straightforward. Here's a step-by-step guide:

Locate the input field on the calculator.
Enter a value between -1 and 1 (inclusive) into the input field. This is the cosine value for which you want to find the inverse.
Press the "Calculate" or "Compute" button.
The calculator will display the result, typically in both radians and degrees.

It's important to note that the input value must be between -1 and 1 because the cosine function's range is limited to these values. Any number outside this range will result in an error or undefined result.

Examples of Using the Inverse Cosine Calculator

Let's look at two practical examples to better understand how to use the inverse cosine calculator:

Example 1: Finding an Angle in a Right Triangle

Suppose you're working on a problem involving a right triangle. You know that the cosine of one of the angles is 0.5, and you need to find the measure of that angle.

Enter 0.5 into the inverse cosine calculator.
Press the calculate button.
The calculator will return approximately 1.0472 radians or 60 degrees.

This means that the angle whose cosine is 0.5 measures 60 degrees or about 1.0472 radians.

Example 2: Verifying Trigonometric Identities

Inverse cosine calculators can also be useful for verifying trigonometric identities. Let's say you want to confirm that cos(arccos(x)) = x for any value of x between -1 and 1.

Choose a value for x, say 0.75.
Enter 0.75 into the inverse cosine calculator.
The calculator will return approximately 0.7227 radians or 41.41 degrees.
Now, if you were to use a regular cosine calculator and input 0.7227 radians (or 41.41 degrees), you should get a result very close to 0.75, thus verifying the identity.

The Importance of Radians and Degrees

When using an inverse cosine calculator, you'll often see results given in both radians and degrees. Understanding both is crucial for effective use of the calculator.

Radians

Radians are the standard unit of angular measurement in many areas of mathematics. One radian is defined as the angle subtended at the center of a circle by an arc equal in length to the radius of the circle. There are approximately 6.28318 (2π) radians in a complete circle.

Degrees

Degrees are more commonly used in everyday applications. A complete circle is divided into 360 degrees. Many people find degrees easier to visualize, which is why inverse cosine calculators often provide results in both units.

To convert between radians and degrees:

1 radian ≈ 57.2958 degrees
1 degree ≈ 0.0174533 radians

Applications of the Inverse Cosine Calculator

The inverse cosine calculator finds applications in various fields:

Trigonometry: It's fundamental in solving trigonometric equations and identities.
Physics: Used in calculations involving vectors, forces, and motion.
Engineering: Applied in structural analysis and design.
Navigation: Essential for determining angles and directions.
Computer Graphics: Used in 3D modeling and animation.

Limitations

While the inverse cosine calculator is a powerful tool, it's important to be aware of its limitations:

Input Range: The calculator only accepts values between -1 and 1, inclusive. Any value outside this range will result in an error or undefined result.
Precision: Digital calculators may have slight rounding errors, especially when dealing with irrational numbers.
Principal Value: The inverse cosine function returns the principal value, which means it only gives angles in the range [0, π] radians or [0°, 180°].

Advanced Features of Some Inverse Cosine Calculators

Some advanced inverse cosine calculators offer additional features:

Graphing capabilities: These allow users to visualize the inverse cosine function.
Step-by-step solutions: Helpful for educational purposes, showing the process of calculation.
Conversion between different angle units: Some calculators can convert between radians, degrees, and gradians.

Tips for Using the Inverse Cosine Calculator

To get the most out of your inverse cosine calculator:

Always check your input: Ensure you're entering a value between -1 and 1.
Understand the output: Know whether you need the result in radians or degrees for your specific problem.
Use it in conjunction with other trigonometric calculators: Often, complex problems require multiple calculations.
Practice with various inputs: This will help you develop an intuition for the relationship between cosine values and angles.

Common Mistakes

When using an inverse cosine calculator, be wary of these common errors:

Inputting values outside the -1 to 1 range.
Confusing inverse cosine (arccos) with the reciprocal of cosine (sec).
Forgetting to convert between radians and degrees when necessary.
Misinterpreting the result when solving real-world problems.

References

study.com/academy/lesson/arccosine-definition-lesson-quiz.html. (n.d.). study.com/academy/lesson/arccosine-definition-lesson-quiz.html
What is the difference between y = arccos x and y = cos-1 x? - GeeksforGeeks. (2022, April 22). GeeksforGeeks. geeksforgeeks.org/what-is-the-difference-between-y-arccos-x-and-y-cos-1-x/