Partial Sum Calculator
The partial sum calculator helps you calculate the partial sum of arithmetic as well as geometric series.
It is also called as sum of series calculator.
Choose the series type from the drop-down menu.
Enter the first term, common difference, and number of terms if you choose the arithmetic series. You will be able to determine the arithmetic series sum.
Enter the first term, common ratio, and number of terms if you choose the geometric series. You will be able to determine the finite geometric series sum.
A partial sum refers to a series of sums in a given sequence. It starts with the first element and progresses by adding each subsequent element to the previous sum.
An arithmetic series is the sum of the terms in an arithmetic sequence. The nth partial sum can be calculated using the formula Sn = n(a1+an)/2.
A geometric series is the sum of terms in a geometric sequence. The nth partial sum of a geometric sequence can be calculated using the first term a1 and common ratio r as Sn=a1(1−rn)1−r.
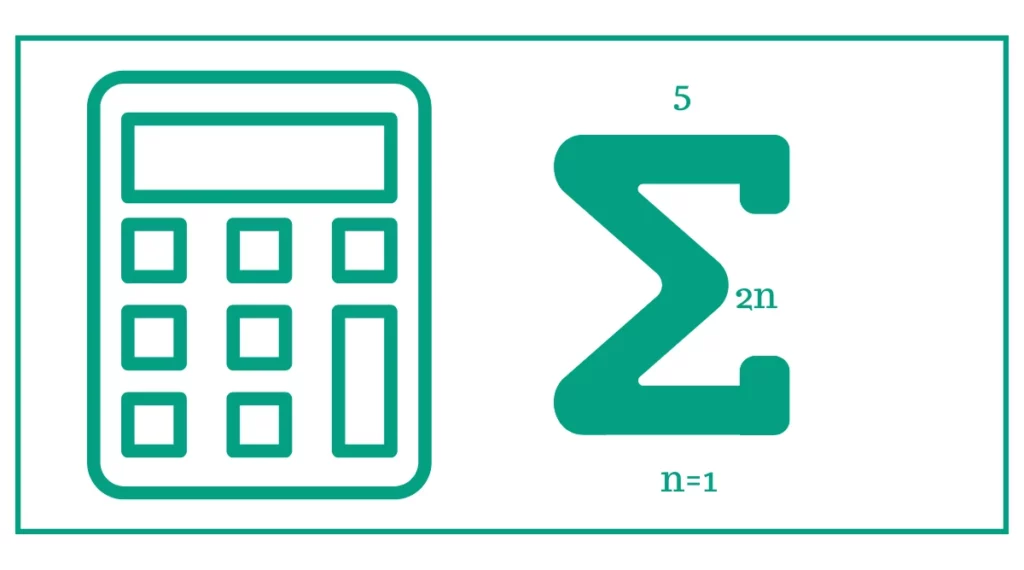
You might want to calculate the unit rate or determine the method for percent-fraction conversion.
What is a Sum Calculator?
A sum calculator is an online tool designed to compute the sum of a series of numbers. It can handle different types of series, including arithmetic and geometric sequences. This calculator allows users to input the necessary parameters and quickly obtain the sum of the series, saving time and reducing the chance of calculation errors.
Types of Series Supported by This Calculator
Arithmetic Series
An arithmetic series is a sequence of numbers where the difference between any two consecutive terms is constant. This constant difference is known as the common difference. The formula for the sum of an arithmetic series is:
Sₙ = (n / 2) * (2a + (n – 1)d)
Where:
- Sₙ is the sum of the series
- n is the number of terms
- a is the first term
- d is the common difference
Geometric Series
A geometric series is a sequence of numbers where each term after the first is found by multiplying the previous term by a fixed, non-zero number called the common ratio. The formula for the sum of a finite geometric series is:
Sₙ = a * (1 – rⁿ) / (1 – r)
Where:
- Sₙ is the sum of the series
- a is the first term
- r is the common ratio
- n is the number of terms
For infinite geometric series where |r| < 1, the sum formula is:
S∞ = a / (1 – r)
How to Use the Sum Calculator
Using this online calculator to find the sum of a series is straightforward. Follow these steps:
- Select the series type (arithmetic or geometric) from the dropdown menu.
- Enter the first term (a) of the sequence.
- Input the common difference (d) for arithmetic series or common ratio (r) for geometric series.
- Specify the number of terms (n) in the series.
- Click the “Calculate” button to obtain the result.
The calculator will display the sum of the series based on the provided inputs.
Examples of Sum Calculations
Example 1: Arithmetic Series
Let’s calculate the sum of an arithmetic series with the following parameters:
- First term (a) = 3
- Common difference (d) = 2
- Number of terms (n) = 10
Using the formula: Sₙ = (n / 2) * (2a + (n – 1)d)
S₁₀ = (10 / 2) * (2 * 3 + (10 – 1) * 2)
S₁₀ = 5 * (6 + 18)
S₁₀ = 5 * 24
S₁₀ = 120
The sum of this arithmetic series is 120.
Example 2: Geometric Series
Now, let’s calculate the sum of a geometric series with these parameters:
- First term (a) = 2
- Common ratio (r) = 3
- Number of terms (n) = 5
Using the formula: Sₙ = a * (1 – rⁿ) / (1 – r)
S₅ = 2 * (1 – 3⁵) / (1 – 3)
S₅ = 2 * (1 – 243) / (-2)
S₅ = 2 * (-242) / (-2)
S₅ = 242
The sum of this geometric series is 242.
Applications of Series and Sums
Understanding series and their sums has numerous practical applications across various fields:
- Finance: Calculating compound interest, annuities, and loan payments.
- Physics: Analyzing sequences in motion, waves, and energy calculations.
- Engineering: Designing structures, signal processing, and control systems.
- Computer Science: Analyzing algorithm complexity and data structures.
- Statistics: Probability distributions and data analysis.
Benefits of Using an Online Sum Calculator
- Accuracy: Eliminates human error in complex calculations.
- Time-saving: Quickly computes sums for large series.
- Educational tool: Helps students understand series concepts.
- Versatility: Handles both arithmetic and geometric series.
- Accessibility: Available online for free, anytime and anywhere.
Advanced Features of the Sum Calculator
While this calculator focuses on arithmetic and geometric series, it’s worth noting that there are more complex series in mathematics. Some advanced calculators may offer additional features such as:
- Partial sum calculations
- Infinite series analysis
- Power series computations
- Convergence tests for infinite series
- Graphical representations of series
Understanding Partial Sums
A partial sum is the sum of a finite number of terms in a series. For instance, in an arithmetic series 2, 4, 6, 8, 10, …, the partial sums would be:
- S₁ = 2
- S₂ = 2 + 4 = 6
- S₃ = 2 + 4 + 6 = 12
- S₄ = 2 + 4 + 6 + 8 = 20
Partial sums are crucial in understanding the behavior of infinite series and their convergence.
Convergence of Infinite Series
For infinite series, particularly geometric series, the concept of convergence is essential. An infinite series converges if the sequence of its partial sums approaches a finite limit. For a geometric series, this occurs when the absolute value of the common ratio is less than 1 (|r| < 1).
Tips for Using the Sum Calculator Effectively
- Double-check your inputs: Ensure you’ve entered the correct values for the first term, common difference/ratio, and number of terms.
- Understand the limitations: This calculator is designed for arithmetic and geometric series. For more complex series, you may need advanced mathematical software.
- Use it as a learning tool: Try different values and observe how changes in parameters affect the sum.
- Verify results: For simple series, try calculating the sum manually and compare it with the calculator’s result to build confidence in your understanding.
References
- 30.6 Computing Series Partial Sums. (n.d.). 30.6 Computing Series Partial Sums. ocw.mit.edu/ans7870/18/18.013a/textbook/HTML/chapter30/section06.html
- van der Vaart, A. W., & Wellner, J. A. (1996). Partial-Sum Processes. Weak Convergence and Empirical Processes, 225–231. doi.org/10.1007/978-1-4757-2545-2_24
- Chlebus, E. (2009). An approximate formula for a partial sum of the divergent p-series. Applied Mathematics Letters, 22(5), 732-737.